Kerasを使ったRNNによる時系列データ予測の試み
概要
最近ではKaggleの上位陣もRNNでの予測でいい結果を出しているという噂を聞いて興味があり、KerasにてRNNを利用した時系列の予測を行ってみました。
結論としてはそこまで望ましい精度は出なかったのですが(自分のやり方の問題の可能性あり)、取り組みのメモと今後の課題を忘れないために書いておきます。
※今記事では十分に検証しきれなかった部分がありましたので続きは以下です。
データに関して
データセットは航空会社の国際線での乗客数の時系列データを用います。
分析
データの確認
まずはどういったデータなのかを確認します。
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
%matplotlib inline
df = pd.read_csv("international-airline-passengers.csv", skipfooter=3)
df.plot()
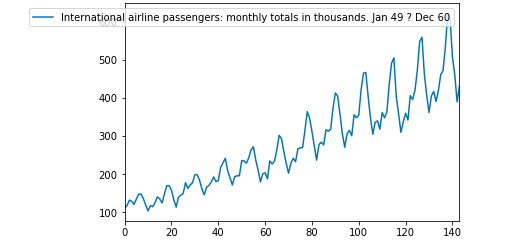
トレンドを持って増加していくようなデータになっています。
年間の中で周期性があって、定期的にベースが上がっていくようなデータでありそうです。
階差をとって正規化
トレンドのあるデータなので、時系列データの分析を行う際によくやられる階差を取るという処理を行います。
RNNでの予測の際に必要なのかは明確には分かっていませんが、参考した記事では行われていたので同様に行います[1]。
またRNNでデータを入れるために配列の位置をずらしたデータを用意します。これが教師用データになります。与えられたt-1のデータでt時点を予測するようなイメージです。
#乗客数データのみ取り出す
passenger = np.array(df.iloc[:, 1].astype('float32'))
#1階差をとる
def difference(data):
diffed = data[1:] - data[:-1]
return diffed
#配列をずらして目的変数を作成
def shift(data):
X = data[:-1]
y = data[1:]
return X, y
X_d, y_d = shift(difference(passenger)) #階差をとったデータ
この段階で予測用と検証用にデータを分けます。
### データの分割 from sklearn.model_selection import train_test_split X_d_train, X_d_val, y_d_train, y_d_val = train_test_split(X_d, y_d, test_size = 0.3, shuffle = False)
またRNNではデータの取りうる範囲が0~1でないと適切に予測できないため正規化を行います。
from sklearn.preprocessing import MinMaxScaler #正規化 sclr_x = MinMaxScaler(feature_range=(0, 1)) sclr_y = MinMaxScaler(feature_range=(0, 1)) X_d_train = sclr_x.fit_transform(X_d_train.reshape(-1, 1)) X_d_val = sclr_x.transform(X_d_val.reshape(-1, 1)) y_d_train = sclr_y.fit_transform(y_d_train.reshape(-1, 1)) y_d_val = sclr_y.transform(y_d_val.reshape(-1, 1))
そして最終的にkerasのRNNで使えるデータに変換します。 今回は一回の予測に1つの状態しか使わないようにしていますが、windowのサイズを変えることで、何個前の状態を使うかを指定することで精度等は変わると思います。
# データ変換
def convert(X, y, ws = 1, dim = 1):
data = []
target = []
#windowサイズが1の場合は全部のデータを使う
#そうでない場合は、wsで全てのデータが収まる範囲で使う
if(ws == 1):
itr = len(X)
else:
itr = len(X) - ws
for i in range(itr):
data.append(X[i: i + ws])
target.append(y[i])
# データの整形
data = np.array(data).reshape(len(data), ws, dim)
target = np.array(target).reshape(-1,1)
return data, target
#変換
X_train_c, y_train_c = convert(X_d_train, y_d_train,1, 1)
X_val_c, y_val_c = convert(X_d_val, y_d_val, 1, 1)
モデルの定義
モデルは以下のように定義しました。
import keras
from keras.layers import Input, Embedding, LSTM, Dense
from keras.models import Model
from keras.optimizers import Adam
from keras.layers.wrappers import Bidirectional
#モデル設定
main_input = Input(shape=(X_train_c.shape[1], X_train_c.shape[2]),
dtype='float32',
batch_shape = (1, X_train_c.shape[1], 1),
name='main_input')
out = Bidirectional(LSTM(8, return_sequences = True, stateful = True, activation='tanh'))(main_input)
out = Bidirectional(LSTM(16, stateful = True, activation='tanh'))(out)
main_output = Dense(1, activation='linear', name='output')(out)
model = Model(inputs=[main_input], outputs=[main_output])
model.compile(loss="mse", optimizer=Adam())
階層は2階層で双方向性(Bidirectional)、statefulを入れています。
学習
学習は1エポック毎にstateをリセットする形で行いました。
#学習
batch_size = 1
n_epoch = 2000
log_loss = np.zeros(n_epoch)
log_val_loss = np.zeros(n_epoch)
models = []
for i in range(n_epoch):
res = model.fit(X_train_c, y_train_c, batch_size = batch_size,
epochs = 1, validation_data=(X_val_c, y_val_c), verbose = 2, shuffle = False)
#ロスを保存
log_loss[i] = res.history['loss'][0]
log_val_loss[i] = res.history['val_loss'][0]
models.append(res)
model.reset_states() #毎回sateをリセット
ロスの推移は以下で確認。
loss_df = pd.DataFrame([log_loss, log_val_loss]).T loss_df.columns = ["loss", "val_loss"] loss_df.plot()

バリデーションロスが一番低いモデルを使います。
print(np.argsort(log_val_loss)[0]) print(np.argsort(log_loss)[0]) best_model = models[np.argsort(log_val_loss)[0]].model
予測
予測は一個後を予測する方法と、予測結果を使って予測させる方法の二種類を試しました。
#各予測にvalidationデータを使う
def pred_val(model, X, X_val):
model.reset_states()
length = len(X_val)
prediction_train = np.zeros(len(X))
prediction = np.zeros(length)
#train分まず予測する
for i in range(len(X)):
prediction_train[i] = model.predict(X[i].reshape(1,-1,1))[0]
#特定期間さきまで予測
for i in range(length):
prediction[i] = model.predict(X_val_c[i].reshape(1,-1,1))[0]
model.reset_states()
return np.hstack((prediction_train, prediction))
#各予測に予測結果を使う
def pred_pred_data(model, X, X_val):
model.reset_states()
length = len(X_val)
prediction_train = np.zeros(len(X))
prediction = np.zeros(length)
#train分まず予測する
for i in range(len(X)):
prediction_train[i] = model.predict(X[i].reshape(1,-1,1))[0]
tmp = X[len(X) - 1, :, :].reshape(1,-1,1)#学習データの最後の値から予測していく
#特定期間さきまで予測
for i in range(length):
prediction[i] = model.predict(tmp)[0]
#次に予測に使うデータを更新
#tmp = tmp[0, 1:, 0]
#tmp = np.append(tmp, prediction[i]).reshape(1,-1,1)
tmp = prediction[i].reshape(1,-1,1)
model.reset_states()
return np.hstack((prediction_train, prediction))
検証用のデータも予測にいかし、一個先の値を予測させた結果です。
#validationデータで予測 pred = pred_val(best_model, X_train_c, X_val_c) res = np.vstack((X_d_train, X_d_val))[:, 0] pd.DataFrame(np.vstack((res,pred)).T).plot() pow(pred[-43:] - X_d_val[:, 0], 2).mean()

予測結果で予測させた結果です。
#予測結果で予測 pred2 = pred_pred_data(best_model, X_train_c, X_val_c) res2 = np.vstack((X_d_train, X_d_val))[:, 0] pd.DataFrame(np.vstack((res2, pred2)).T).plot() pow(pred2[-43:] - X_d_val[:, 0], 2).mean()

以上二つを比べると、どちらも良くないですが、当たり前ですが比較的まともなのは、検証用データを活かして一つ先だけを予測させたほうです。
せっかくなので、検証用データをいかした予測の方で、正規化を戻して、階差も戻してみるとどうなるか確かめてみます。
#valデータを使ったデータを使う
pred_inv = sclr_x.inverse_transform(pred.reshape(-1, 1))
#差分を予測しているので足し合わせていく
out = np.zeros(pred_inv.shape[0] + 1)
out[0] = (passenger[0])
for i in range(len(pred_inv[:, 0])):
out[i + 1] = (passenger[i] + pred_inv[i])
#実績と予測の可視化
pd.DataFrame(np.vstack((passenger[:143], out)).T).plot()

段々とズレていくことが見えてますね・・・。ちょっと残念な結果です。
平均絶対誤差はと言うと、
#平均絶対誤差 abs(passenger[:143] - out).mean()
23.928050769405846でした。。。
おまけ(Rのprophetで予測)
facebookが開発している時系列予測のライブラリのprophetで予測するとどうなのかも検証してみました。
以下コードです。
#ライブラリ
library(prophet)
library(tidyverse)
#データ読込
df <-read.csv("international-airline-passengers.csv", stringsAsFactors = FALSE)
#データ前処理
names(df)[1] <- "ds"
names(df)[2] <- "y"
df$ds <- paste(df$ds, "-01", sep = "")
df$ds <- as.Date(df$ds)
df <- na.omit(df)
df$y <- log(df$y)
#plot(df$y)
#テストデータと検証データの分割
df_train <- df[(1:99), ]
df_val <- df[-(1:99), ]
#予測
m <- prophet(df_train,
yearly.seasonality = TRUE,
weekly.seasonality = FALSE,
daily.seasonality = FALSE)
future <- make_future_dataframe(m, periods = 45, freq = 'month')
forecast <- predict(m, future)
#可視化
plot(m, forecast)
#prophet_plot_components(m, forecast)
#精度検証
res <- forecast %>% select(ds, yhat)
res <- res[-(1:99), ]
#平均二乗誤差
mean(abs(exp(res$yhat) - exp(df_val$y)))
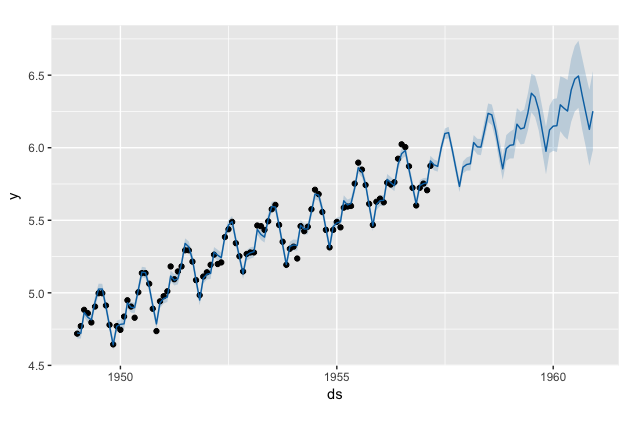
幅で予測できるのはとてもいいですね。
また単純に突っ込んだだけのデータにも関わらず、精度の方は42.80722と負けてはいますが、prophetの方での予測時には検証用のデータは一切使っていないので、負けるのは仕方ないと思います。
おそらく検証用のデータを使って一個ずつ先を予測させたら精度は大分あがるのではないかと思います。
課題
今回の取り組みの課題は以下です。
- 他の手法より劣る精度しか出なかった
今回の主要な試みではRNNを使いました。またprophetで適当にデータを入れて予測した結果とを最後に比べて見ましたがRNNが十分に勝っているとはいえません(比較の仕方は良くないにしろ)。
現時点ではやり方が悪いのか、どこに問題があるのか分かっていませんが、このままではRNNを構築する労力に見合わないのが現状かなと思います(多分prophetの30倍くらい大変)。
もちろんデータがより大規模になったり、多変数で予測するようなデータ構造であったり、特徴量の作り方を工夫するとより良い精度が出るかもしれません(Kaggleで上位の方がRNNを使っていることを考慮するとおそらくこういうことだと思います)。
- 予測結果を使った予測でいい精度がでなかった
実務では現在から一ヶ月間で観測したい事象がどういった推移になるか予測したいと思います(例えば、売上など)。すると長い予測を得るには予測した結果でその次を予測し、その結果で次を予測しの繰り返しで、やる必要があると思います(検証用のデータを活かして一個先を予測してくのは利用する際には現実的ではない)。
しかし今回のやり方では望ましい精度が出ませんでした。
参考にした資料[1]では予測した結果を使ってもなかなかいい精度が出ているので、もしかしたらやり方が間違っているかもしれません。
今後これらを改善できないか、考えていきたいと思います。
まとめ
なかなかRNNでの時系列予測は簡単にはいかなさそうです。
今後はprophet等のより楽なアプローチに対してどうしたらRNNの優位性がでるのか、引き続き検証したいと思います。
突っ込みどころ等ありましたらコメントお願いします。
参考
[1] chainerによるLSTMを用いた時系列予測 - Qiita
[2] Stateful LSTM in Keras – Philippe Remy – My Blog.
[3] Multi-step Time Series Forecasting with Long Short-Term Memory Networks in Python